前回のブログにてSiC耐火物の曲げ強さについて説明いたしました。では、同じ材質で幅や厚みが違う場合強さはどう変化するのかというのを今回ご説明致します。前回ブログにも出てきましたが、耐火物・セラミックスの3点曲げ強さσb3(Mpa)の公式は σb3=3PL÷(2wt2) となります。
- P:試験片が破壊したときの最大荷重(N)
- L:支点間距離(mm)
- w:試験片の幅(mm)
- t:試験片の厚さ(mm)
*「JISハンドブック セラミックス2010」より引用。
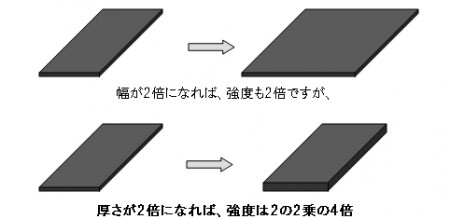
この方程式をP(試験片が破壊したときの最大荷重)で解くと、P=σb3×2wt2÷3L となります。ここで式を良く見ると、試験片の厚さ “t” が2乗になっています。即ち同じ材質で同じ曲げ強さ”σb3″の耐火物は、厚さが2倍になれば強さは2倍の2乗の4倍になります。因みに幅が2倍になった場合はそのまま強さも2倍となります。
また感覚的にもお解りになるかと思いますが、式の通り支点間距離 “L” が2倍になると、1/2の荷重 “P” で折れる事となり、即ち耐火物の強さも1/2に弱くなります。